I heard of these random walks from my number-theorist colleague Andrei Jorza who gave me a probabilistic translation of some observations in number theory. What follows is rather a variation on that theme.
There is a whole family of such walks, parametrized by a complex number $\newcommand{\ii}{\boldsymbol{i}}$ $\rho=\cos \theta +\ii \sin\theta$, $\theta\in [0,\pi]$, $\ii=\sqrt{-1}$.
This is discrete time walk on the configuration space $\newcommand{\lan}{\langle}$ $\newcommand{\ran}{\rangle}$
$$ \eC_\rho:= L[\rho] \times C(\rho,-\rho), $$
where $C(\rho,-\rho)$ is the subgroup of $S^1$ generated by $\pm\rho$, i.e.,
$$ C(\rho,-\rho)=\bigl\{\; \pm \rho^k;\;\;k\in\bZ \;\bigr\},$$
and $L[\rho]\subset \bC$ is the additive subgroup of $\bC$ generated by the elements $\rho^n$, $n\in\bZ_{\geq 0}$.
The state of the walk at time $n$ is given by a pair of random variables $(X_n, V_n)$, where one should think of $X_n\in L[\rho]$ as describing the "position'' and $V_n\in G(\rho,-\rho)$ as describing the ``velocity'' at time $n$.
Here is how the random walk takes place. Suppose that at time $n$ we are in the configuration $(X_n, V_n)$. To decide where to go next, toss a fair coin. If a the Head shows up then
$$V_{n+1}=\rho V_n,\;\; X_{n+1}= X_n+V_{n+1}. $$
Otherwise,
$$ V_{n+1}=-\rho V_n,\;\; X_{n+1}= X_n+V_{n+1}. $$
More abstractly, we are given a probability space $(\Omega,\eF,\bP)$ and a sequence of independent, identically distributed variables
$$ S_n:\Omega\to\{-1,1\},\;\;\bP[S_n=\pm 1]=\frac{1}{2},\;\;n\in\bZ_{\geq 0}. $$
If we set
$$
\whS_n:=\prod_{k=1}^nS_k, $$
then we have
$$
V_n= \whS_n \rho^n,\;\;X_n=\sum_{k=1}^n V_n=\sum_{k=1}^n \whS_k\rho_k.
$$
Observing that
$$\bE[\whS_k]=0,\;\;\var[\whS_k]=\prod_{j=1}^k\var[S_j]=1, $$ we deduce
$$\bE[X_n]=0,\;\;\var[S_n]=\bE[X_n\bar{X}_n] $$
$$=\sum_{j,k=1}^n \bE[ \whS_j\whS_k]\rho^{k-j}=\sum_{j=1}^n \bE[ \whS_j^2]+2\sum_{1\leq j<k\leq}^n \bE[ \whS_j\whS_k]\rho^{k-j}=n. $$
Example 1. Suppose that $\theta=\frac{\pi}{2}$ so that $\rho=\ii$. In this case $L[\rho]$ is the lattice $\bZ^2\subset \bC$ and $G(\ii,-\ii)$ is the group of forth order roots of $1$. At time $n=0$, the moving particle is at the origin facing East,. turns right or left (in this case North/South) with equal probability. Once reaches a new intersection, it turns right/left with equal probability. The following MAPLE generated animation a loop describes a 90-step portion of one such walk.
This is somewhat typical of what one observes in general.
Example 2. Suppose that $\theta =\frac{\pi}{3}$. In this case $G(\rho,-\rho)$ is the group of 6th order roots of $1$ and $L[\rho]$ is a lattice in $\bC$. The following MAPLE generated animation depicts a 90 step portion of such a walk and the patterns you observe are typical.
Example 3. Assume that the angle $\theta$ is small and $\frac{\theta}{\pi}$ is not rational, say $\cos \theta=0.95$. The animation below depicts a 90-step stretch of such a walk.
Example 4. For comparison, I have included an animation of a 90-step segment of the usual uniform random walk on $\bZ^2$.
Clearly, I am interested to figure out what is happening and I have a hard time asking a good question. A first question that comes to my mind would be to find statistical invariants that would distinguish the random walk in Example 1 from the random walk in Example 4. I will refer to them as $RW_1$ and $RW_4$
Clear each of these two walks surround many unit squares with vertices in the lattice $\bZ^2$. For $j=1,4$ will denote by $s_j(n)$ the expected number of unit squares surrounded by a walk of $RW_j$ of length $n$.. Which grows faster as $n\to\infty$, $s_1(n)$ or $s_4(n)$?
I will probably update this posting as I get more ideas, but maybe this shot in the dark will initiate a conversation and will suggest other, better questions.





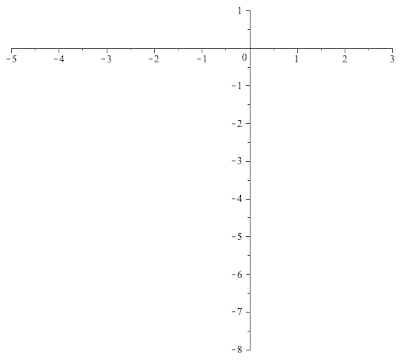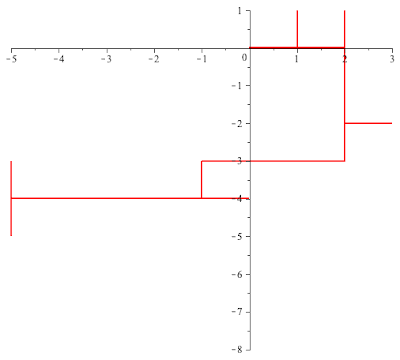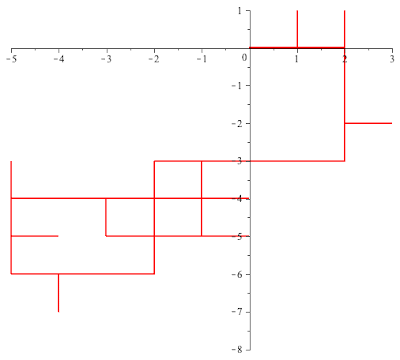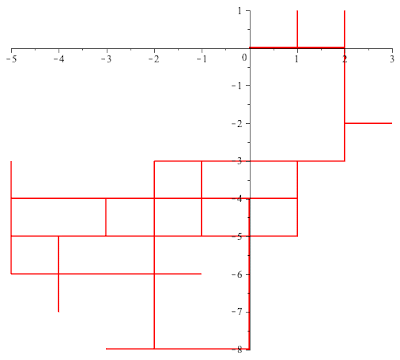
No comments:
Post a Comment