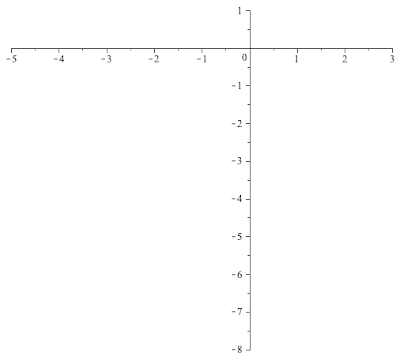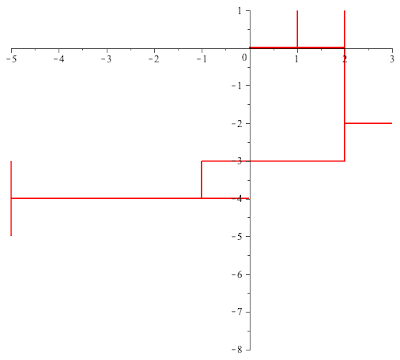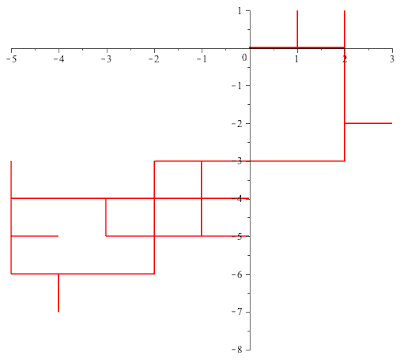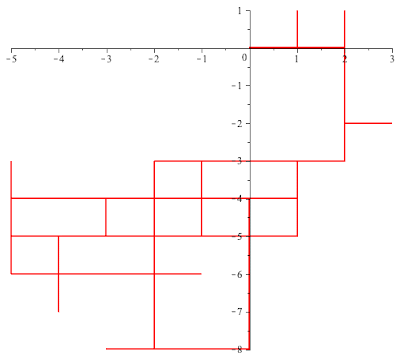Wednesday, November 25, 2015
Thursday, November 19, 2015
On a class of random walks
I heard of these random walks from my number-theorist colleague Andrei Jorza who gave me a probabilistic translation of some observations in number theory. What follows is rather a variation on that theme.
There is a whole family of such walks, parametrized by a complex number $\newcommand{\ii}{\boldsymbol{i}}$ $\rho=\cos \theta +\ii \sin\theta$, $\theta\in [0,\pi]$, $\ii=\sqrt{-1}$.
This is discrete time walk on the configuration space $\newcommand{\lan}{\langle}$ $\newcommand{\ran}{\rangle}$
$$ \eC_\rho:= L[\rho] \times C(\rho,-\rho), $$
where $C(\rho,-\rho)$ is the subgroup of $S^1$ generated by $\pm\rho$, i.e.,
$$ C(\rho,-\rho)=\bigl\{\; \pm \rho^k;\;\;k\in\bZ \;\bigr\},$$
and $L[\rho]\subset \bC$ is the additive subgroup of $\bC$ generated by the elements $\rho^n$, $n\in\bZ_{\geq 0}$.
The state of the walk at time $n$ is given by a pair of random variables $(X_n, V_n)$, where one should think of $X_n\in L[\rho]$ as describing the "position'' and $V_n\in G(\rho,-\rho)$ as describing the ``velocity'' at time $n$.
Here is how the random walk takes place. Suppose that at time $n$ we are in the configuration $(X_n, V_n)$. To decide where to go next, toss a fair coin. If a the Head shows up then
$$V_{n+1}=\rho V_n,\;\; X_{n+1}= X_n+V_{n+1}. $$
Otherwise,
$$ V_{n+1}=-\rho V_n,\;\; X_{n+1}= X_n+V_{n+1}. $$
More abstractly, we are given a probability space $(\Omega,\eF,\bP)$ and a sequence of independent, identically distributed variables
$$ S_n:\Omega\to\{-1,1\},\;\;\bP[S_n=\pm 1]=\frac{1}{2},\;\;n\in\bZ_{\geq 0}. $$
If we set
$$
\whS_n:=\prod_{k=1}^nS_k, $$
then we have
$$
V_n= \whS_n \rho^n,\;\;X_n=\sum_{k=1}^n V_n=\sum_{k=1}^n \whS_k\rho_k.
$$
Observing that
$$\bE[\whS_k]=0,\;\;\var[\whS_k]=\prod_{j=1}^k\var[S_j]=1, $$ we deduce
$$\bE[X_n]=0,\;\;\var[S_n]=\bE[X_n\bar{X}_n] $$
$$=\sum_{j,k=1}^n \bE[ \whS_j\whS_k]\rho^{k-j}=\sum_{j=1}^n \bE[ \whS_j^2]+2\sum_{1\leq j<k\leq}^n \bE[ \whS_j\whS_k]\rho^{k-j}=n. $$
Example 1. Suppose that $\theta=\frac{\pi}{2}$ so that $\rho=\ii$. In this case $L[\rho]$ is the lattice $\bZ^2\subset \bC$ and $G(\ii,-\ii)$ is the group of forth order roots of $1$. At time $n=0$, the moving particle is at the origin facing East,. turns right or left (in this case North/South) with equal probability. Once reaches a new intersection, it turns right/left with equal probability. The following MAPLE generated animation a loop describes a 90-step portion of one such walk.
This is somewhat typical of what one observes in general.
Example 2. Suppose that $\theta =\frac{\pi}{3}$. In this case $G(\rho,-\rho)$ is the group of 6th order roots of $1$ and $L[\rho]$ is a lattice in $\bC$. The following MAPLE generated animation depicts a 90 step portion of such a walk and the patterns you observe are typical.
Example 3. Assume that the angle $\theta$ is small and $\frac{\theta}{\pi}$ is not rational, say $\cos \theta=0.95$. The animation below depicts a 90-step stretch of such a walk.
Example 4. For comparison, I have included an animation of a 90-step segment of the usual uniform random walk on $\bZ^2$.
Clearly, I am interested to figure out what is happening and I have a hard time asking a good question. A first question that comes to my mind would be to find statistical invariants that would distinguish the random walk in Example 1 from the random walk in Example 4. I will refer to them as $RW_1$ and $RW_4$
Clear each of these two walks surround many unit squares with vertices in the lattice $\bZ^2$. For $j=1,4$ will denote by $s_j(n)$ the expected number of unit squares surrounded by a walk of $RW_j$ of length $n$.. Which grows faster as $n\to\infty$, $s_1(n)$ or $s_4(n)$?
I will probably update this posting as I get more ideas, but maybe this shot in the dark will initiate a conversation and will suggest other, better questions.
Sunday, November 15, 2015
Tuesday, November 10, 2015
Random subdivisions of an interval
This is a classical problem, but I find it very appealing.
Drop $n$ points $X_1,\dotsc, X_n$ at random in the unit interval, uniformly and independently. These points divide the interval into $n+1$ sub-intervals. Their lengths are called the spacings of the subdivision. What is the expected length of the longest of these intervals? What is its asymptotic behavior for $n$ large?
I was surprised to find out that the problem of finding the expectation of the largest segment was solved in late 19th century. What follows is a more detailed presentation of the arguments in Sec. 6.3 of the book Order Statistics by H.A. David and H.N. Nagaraja.
If you read French, you can click here to see what P. Levy had to say about this problem back in 1939.
Relabel by $Y_1,\dotsc, Y_n$, the points $\{X_1,\dotsc, X_n\}\subset [0,1]$ so that $Y_1\leq \cdots \leq Y_n$. We set
$$ Y_0=0,\;\;Y_{n+1}=1,\;\;\;\;L_n= \max_{1\leq i\leq n+1} Y_i-Y_{i-1},.$$
We want to determine the expectation $\newcommand{\bE}{\mathbb{E}}$ $E_n$ of $L_n$.
The probability distribution of $\vec{X}=(X_1,\dotsc, X_n)$ $\newcommand{\bone}{\boldsymbol{1}}$ is
$$ p_{\vec{X}}(dx)=\bone_{C_n}(x_1,\dotsc, x_n) dx_1\cdots dx_n, \;\;C_n=[0,1]^n, $$
where $\bone_A$ denotes the indicator function of a subset $A$ of a given set $S$.
The probability distribution of $\vec{Y}=(Y_1,\dotsc, Y_n)$ is
$$p_{\vec{Y}}(dy)= n! \bone_{T_n}(y_1,\dotsc, y_n) dy_1\cdots dy_n, $$
where $T_n$ is the simplex $\newcommand{\bR}{\mathbb{R}}$
$$ T_n=\bigl\{ y\in\bR^n;\;\;0\leq y_1\leq \cdots \leq y_n\leq 1\,\bigr\}. $$
The spacings are the lengths of the $n+1$ segments that the points $Y_1,\dotsc, Y_n$ determine on $[0,1]$
$$ S_i= Y_{i}-Y_{i-1},\;\; i=1,\dotsc, n+1, $$
where $Y_{n+1}:=1$. The resulting map $\vec{Y}\to\vec{S}=\vec{S}(\vec{Y})$ induces a linear bijection
$$ T_n\to \Delta_n=\bigl\{\, (s_1,\dotsc, s_{n+1})\in\bR_{\geq 0}^{n+1};\;\;s_1+\cdots+s_{n+1}=1\,\bigr\}. $$
This shows that the probability density is $\DeclareMathOperator{\vol}{vol}$
$$p_{\vec{S}}(ds) =\frac{1}{\vol(\Delta_n)} dV_{\Delta_n}, $$
where $dV_{\Delta_n}$ denote the usual Euclidean volume density on the standard simplex $\Delta_n$. This description shows that the random vector of spacings $\vec{S}$ is exchangeable, i.e., the probability density of $\vec{S}$ is invariant under permutation of the components. Thus the joint probability distribution of any group of $k$ components of $\vec{S}$, $k\leq n$, is the same as the joint distribution of the first $k$-components $S_1,\dotsc, S_k$.
The joint probability distribution of the first $n$ components is
$$ p_n(ds)= n! \bone_{D_n}(s_1,\dotsc,s_n) ds, $$
where $D_n$ is the simplex
$$ D_n=\{\, (s_1,\dotsc, s_n)\in\bR^n_{\geq 0};\;\;s_1+\cdots +s_n\leq 1\,\}. $$
Indeed, $(S_1,\dotsc, S_n)\in D_n$ and
$$ ds=|ds_1\cdots ds_n|=|d y_1\wedge d(y_2-y_{1})\wedge \cdots \wedge d(y_{n}-y_{n-1})|=|dy_1\cdots d y_n|. $$
The joint density of the first $n-1$ components $(S_1, \dotsc, S_{n-1})$ is
$$ p_{n-1}(s_1,\dotsc, s_{n-1}) = n! \int_0^\infty \bone_{D_n}(s_1,\dotsc, s_n) ds_n $$
$$= n! \bone_{D_{n-1}}(s_1,\dotsc, s_{n-1})\int_0^{1-s+1-\cdots-s_{n-1}} ds_n= n! \bone_{D_{n-1}}(s_1,\dotsc, s_{n-1})(1-s_1-\cdots-s_{n-1}) $$
The joint density of the first $(n-2)$ components is
$$ p_{n-2}(s_1,\dots, s_{n-2})=\int_0^\infty p_{n-1}(s_1,\dotsc, s_{n-1}) ds_{n-1} $$
$$ = n!\bone_{D_{n-2}}(s_1,\dotsc, s_{n-2})\int_0^{1-s_1-\cdots-s_{n-2}} (1-s_1-\cdots -s_{n-1}) d s_{n-1} = \frac{n!}{2!} \bone_{D_{n-2}}(s_1,\dotsc, s_{n-2})(1-s_1-\cdots -s_{n-2})^2. $$
Iterating, we deduce that the joint probability density of the the first $k$ variables is
$$ p_k(s_1,\dotsc, s_k) =\frac{n!}{(n-k)!}p_{D_k}(s_1,\dotsc, s_k) (1-s_1-\cdots-s_k)^{n-k}. $$
If $1\leq k\leq n$, then$\newcommand{\bP}{\mathbb{P}}$
$$ \bP[S_1>s,\dotsc, S_k>s]=\frac{n!}{(n-k)!}\int_s^\infty\cdots\int_s^\infty p_{D_k}(s_1,\dotsc, s_k) (1-s_1-\cdots-s_k)^{n-k} ds_1\dotsc ds_k $$
$$=\frac{n!}{(n-k)!}\int_s^1ds_1\int_s^{1-s_1}ds_2\cdots\int_s^{1-s_1-\cdots-s_{k-1}} (1-s_1-\cdots-s_k)_+^{n-k} ds_k =(1-ks)_+^n,\;\;x_+:=\max(x,0).$$
Also
$$ \bP[S_1>s,\dotsc, S_n>s, S_{n+1}>s] = \bP[S_1>s,\dotsc, S_n>s, S_1+S_2+\cdots +S_n\leq 1-s]$$
$$=n!\int_{\substack{s_1,\dotsc s_{n}>s\\ s_1+\cdots +s_{n}\leq 1-s}}ds_1\cdots d s_{n} $$
$$=n!\int_{\substack{s_1,\dotsc s_{n-1}>s\\ s_1+\cdots +s_{n-1}\leq 1-2s}}ds_1\cdots d s_{n-1}\int_s^{1-s-s_1-\cdots -s_{n-1}} d s_n $$
$$= n!\int_{\substack{s_1,\dotsc s_{n-1}>s\\ s_1+\cdots +s_{n-1}\leq 1-2s}} (1-2s-s_1-\cdots -s_{n-1}) ds_1\cdots ds_{n-1} $$
$$=n!\int_{\substack{s_1,\dotsc s_{n-2}>s\\ s_1+\cdots +s_{n-2}\leq 1-3s}}ds_1\cdots ds_{n-2}\int_s^{1-2s-s_1-\cdots -s_{n-2}} (1-2s-s_1-\cdots -s_{n-1}) d s_{n-1} $$
$$=\frac{n!}{2!} \int_{\substack{s_1,\dotsc s_{n-2}>s\\ s_1+\cdots +s_{n-2}\leq 1-3s}} (1-3s-s_1-\cdots -s_{n-2})^2 ds_1\cdots ds_{n-2} $$
$$ =\frac{n!}{2!} \int_{\substack{s_1,\dotsc s_{n-3}>s\\ s_1+\cdots +s_{n-3}\leq 1-4s}} ds_1\cdots ds_{n-3} \int_s^{1-3s -s_1-\cdots -s_{n-3}} (1-3s-s_1-\cdots -s_{n-2})^2ds_{n-2}$$
$$=\frac{n!}{3!} \int_{\substack{s_1,\dotsc s_{n-3}>s\\ s_1+\cdots +s_{n-3}\leq 1-4s}} (1-4s-s_1-\cdots -s_{n-3})^3ds_1\cdots ds_{n-3} $$
$$=\cdots = \bigl(\, 1-(n+1)s\,\bigr)_+^n. $$
With
$$ L_n:=\max_{1\leq i\leq n+1} S_i $$
we have
$$\bP[L_n>s]=\bP\left[\,\bigcup_{i=1}^{n+1}\bigl\lbrace\, S_i>s\,\bigr\rbrace\,\right] $$
(use inclusion-exclusion exchangeability)
$$ = \sum_{k=1}^{n+1}(-1)^{k+1}\binom{n+1}{k} \bP\bigl[\, S_1>s,\dotsc, S_k>s\,\bigr] =\sum_{k=1}^{n+1} \binom{n+1}{k}(1-ks)_+^n .$$
The last equality is sometime known as Whitworth formula and it goes all the way back to 1897. We have
$$ E_n=\bE[L_n]=\int_0^\infty \bP[L_n>s] ds =\sum_{k=1}^{n+1}(-1)^{k+1} \binom{n+1}{k}\int_0^\infty (1-ks)_+^n ds = \sum_{k=1}^{n+1}(-1)^{k+1} \binom{n+1}{k}\int_0^{1/k}(1-ks)^n ds $$
$$=\frac{1}{n+1} \sum_{k=1}^{n+1}(-1)^{k+1} \frac{1}{k} \binom{n+1}{k}=\sum_{k=1}^{n+1}(-1)^{k+1} \frac{1}{k^2} \binom{n}{k-1}. $$
Here is $E_n$ answers for small $n$ (thank you MAPLE)
$$ E_1=\frac{3}{4},\;\;E_2=\frac{11}{18},\;\;E_3=\frac{25}{48},\;\;E_4=\frac{137}{300},\;\; E_5=\frac{49}{120}. $$
It turn out that $L_n$ is highly concentrated around its mean. In the work of P. Levy I mentioned earlier he showed that the random variables $nL_n-\log n$ converges in probability to a random variable $X_\infty$ with probability distribution $\mu$ given by
$$ \mu\bigl(\,(-\infty,x])= \exp\bigl(\,-e^{-x}\,\bigr),\;\;x\geq 0.$$
Moreover
$$\lim_{n\to \infty} \bE[\, nL_n-\log n\,]=\gamma=\bE[X_\infty],\;\;\lim_{n\to \infty}\mathrm{Var}[ nL_n\,]=\frac{\pi^2}{6}=\mathrm{Var}[X_\infty]. $$
$$\frac{n}{\log n} L_n \to 1\;\; \mbox{a.s.} $$
Note that this shows that
$$E_n\sim\frac{\log n}{n}\;\; \mbox{as $n\to \infty$}. $$
I'll stop here, but you can learn more from this paper of Luc Devroye and its copious list of references.
Drop $n$ points $X_1,\dotsc, X_n$ at random in the unit interval, uniformly and independently. These points divide the interval into $n+1$ sub-intervals. Their lengths are called the spacings of the subdivision. What is the expected length of the longest of these intervals? What is its asymptotic behavior for $n$ large?
I was surprised to find out that the problem of finding the expectation of the largest segment was solved in late 19th century. What follows is a more detailed presentation of the arguments in Sec. 6.3 of the book Order Statistics by H.A. David and H.N. Nagaraja.
If you read French, you can click here to see what P. Levy had to say about this problem back in 1939.
Relabel by $Y_1,\dotsc, Y_n$, the points $\{X_1,\dotsc, X_n\}\subset [0,1]$ so that $Y_1\leq \cdots \leq Y_n$. We set
$$ Y_0=0,\;\;Y_{n+1}=1,\;\;\;\;L_n= \max_{1\leq i\leq n+1} Y_i-Y_{i-1},.$$
We want to determine the expectation $\newcommand{\bE}{\mathbb{E}}$ $E_n$ of $L_n$.
The probability distribution of $\vec{X}=(X_1,\dotsc, X_n)$ $\newcommand{\bone}{\boldsymbol{1}}$ is
$$ p_{\vec{X}}(dx)=\bone_{C_n}(x_1,\dotsc, x_n) dx_1\cdots dx_n, \;\;C_n=[0,1]^n, $$
where $\bone_A$ denotes the indicator function of a subset $A$ of a given set $S$.
The probability distribution of $\vec{Y}=(Y_1,\dotsc, Y_n)$ is
$$p_{\vec{Y}}(dy)= n! \bone_{T_n}(y_1,\dotsc, y_n) dy_1\cdots dy_n, $$
where $T_n$ is the simplex $\newcommand{\bR}{\mathbb{R}}$
$$ T_n=\bigl\{ y\in\bR^n;\;\;0\leq y_1\leq \cdots \leq y_n\leq 1\,\bigr\}. $$
The spacings are the lengths of the $n+1$ segments that the points $Y_1,\dotsc, Y_n$ determine on $[0,1]$
$$ S_i= Y_{i}-Y_{i-1},\;\; i=1,\dotsc, n+1, $$
where $Y_{n+1}:=1$. The resulting map $\vec{Y}\to\vec{S}=\vec{S}(\vec{Y})$ induces a linear bijection
$$ T_n\to \Delta_n=\bigl\{\, (s_1,\dotsc, s_{n+1})\in\bR_{\geq 0}^{n+1};\;\;s_1+\cdots+s_{n+1}=1\,\bigr\}. $$
This shows that the probability density is $\DeclareMathOperator{\vol}{vol}$
$$p_{\vec{S}}(ds) =\frac{1}{\vol(\Delta_n)} dV_{\Delta_n}, $$
where $dV_{\Delta_n}$ denote the usual Euclidean volume density on the standard simplex $\Delta_n$. This description shows that the random vector of spacings $\vec{S}$ is exchangeable, i.e., the probability density of $\vec{S}$ is invariant under permutation of the components. Thus the joint probability distribution of any group of $k$ components of $\vec{S}$, $k\leq n$, is the same as the joint distribution of the first $k$-components $S_1,\dotsc, S_k$.
The joint probability distribution of the first $n$ components is
$$ p_n(ds)= n! \bone_{D_n}(s_1,\dotsc,s_n) ds, $$
where $D_n$ is the simplex
$$ D_n=\{\, (s_1,\dotsc, s_n)\in\bR^n_{\geq 0};\;\;s_1+\cdots +s_n\leq 1\,\}. $$
Indeed, $(S_1,\dotsc, S_n)\in D_n$ and
$$ ds=|ds_1\cdots ds_n|=|d y_1\wedge d(y_2-y_{1})\wedge \cdots \wedge d(y_{n}-y_{n-1})|=|dy_1\cdots d y_n|. $$
The joint density of the first $n-1$ components $(S_1, \dotsc, S_{n-1})$ is
$$ p_{n-1}(s_1,\dotsc, s_{n-1}) = n! \int_0^\infty \bone_{D_n}(s_1,\dotsc, s_n) ds_n $$
$$= n! \bone_{D_{n-1}}(s_1,\dotsc, s_{n-1})\int_0^{1-s+1-\cdots-s_{n-1}} ds_n= n! \bone_{D_{n-1}}(s_1,\dotsc, s_{n-1})(1-s_1-\cdots-s_{n-1}) $$
The joint density of the first $(n-2)$ components is
$$ p_{n-2}(s_1,\dots, s_{n-2})=\int_0^\infty p_{n-1}(s_1,\dotsc, s_{n-1}) ds_{n-1} $$
$$ = n!\bone_{D_{n-2}}(s_1,\dotsc, s_{n-2})\int_0^{1-s_1-\cdots-s_{n-2}} (1-s_1-\cdots -s_{n-1}) d s_{n-1} = \frac{n!}{2!} \bone_{D_{n-2}}(s_1,\dotsc, s_{n-2})(1-s_1-\cdots -s_{n-2})^2. $$
Iterating, we deduce that the joint probability density of the the first $k$ variables is
$$ p_k(s_1,\dotsc, s_k) =\frac{n!}{(n-k)!}p_{D_k}(s_1,\dotsc, s_k) (1-s_1-\cdots-s_k)^{n-k}. $$
If $1\leq k\leq n$, then$\newcommand{\bP}{\mathbb{P}}$
$$ \bP[S_1>s,\dotsc, S_k>s]=\frac{n!}{(n-k)!}\int_s^\infty\cdots\int_s^\infty p_{D_k}(s_1,\dotsc, s_k) (1-s_1-\cdots-s_k)^{n-k} ds_1\dotsc ds_k $$
$$=\frac{n!}{(n-k)!}\int_s^1ds_1\int_s^{1-s_1}ds_2\cdots\int_s^{1-s_1-\cdots-s_{k-1}} (1-s_1-\cdots-s_k)_+^{n-k} ds_k =(1-ks)_+^n,\;\;x_+:=\max(x,0).$$
Also
$$ \bP[S_1>s,\dotsc, S_n>s, S_{n+1}>s] = \bP[S_1>s,\dotsc, S_n>s, S_1+S_2+\cdots +S_n\leq 1-s]$$
$$=n!\int_{\substack{s_1,\dotsc s_{n}>s\\ s_1+\cdots +s_{n}\leq 1-s}}ds_1\cdots d s_{n} $$
$$=n!\int_{\substack{s_1,\dotsc s_{n-1}>s\\ s_1+\cdots +s_{n-1}\leq 1-2s}}ds_1\cdots d s_{n-1}\int_s^{1-s-s_1-\cdots -s_{n-1}} d s_n $$
$$= n!\int_{\substack{s_1,\dotsc s_{n-1}>s\\ s_1+\cdots +s_{n-1}\leq 1-2s}} (1-2s-s_1-\cdots -s_{n-1}) ds_1\cdots ds_{n-1} $$
$$=n!\int_{\substack{s_1,\dotsc s_{n-2}>s\\ s_1+\cdots +s_{n-2}\leq 1-3s}}ds_1\cdots ds_{n-2}\int_s^{1-2s-s_1-\cdots -s_{n-2}} (1-2s-s_1-\cdots -s_{n-1}) d s_{n-1} $$
$$=\frac{n!}{2!} \int_{\substack{s_1,\dotsc s_{n-2}>s\\ s_1+\cdots +s_{n-2}\leq 1-3s}} (1-3s-s_1-\cdots -s_{n-2})^2 ds_1\cdots ds_{n-2} $$
$$ =\frac{n!}{2!} \int_{\substack{s_1,\dotsc s_{n-3}>s\\ s_1+\cdots +s_{n-3}\leq 1-4s}} ds_1\cdots ds_{n-3} \int_s^{1-3s -s_1-\cdots -s_{n-3}} (1-3s-s_1-\cdots -s_{n-2})^2ds_{n-2}$$
$$=\frac{n!}{3!} \int_{\substack{s_1,\dotsc s_{n-3}>s\\ s_1+\cdots +s_{n-3}\leq 1-4s}} (1-4s-s_1-\cdots -s_{n-3})^3ds_1\cdots ds_{n-3} $$
$$=\cdots = \bigl(\, 1-(n+1)s\,\bigr)_+^n. $$
With
$$ L_n:=\max_{1\leq i\leq n+1} S_i $$
we have
$$\bP[L_n>s]=\bP\left[\,\bigcup_{i=1}^{n+1}\bigl\lbrace\, S_i>s\,\bigr\rbrace\,\right] $$
(use inclusion-exclusion exchangeability)
$$ = \sum_{k=1}^{n+1}(-1)^{k+1}\binom{n+1}{k} \bP\bigl[\, S_1>s,\dotsc, S_k>s\,\bigr] =\sum_{k=1}^{n+1} \binom{n+1}{k}(1-ks)_+^n .$$
The last equality is sometime known as Whitworth formula and it goes all the way back to 1897. We have
$$ E_n=\bE[L_n]=\int_0^\infty \bP[L_n>s] ds =\sum_{k=1}^{n+1}(-1)^{k+1} \binom{n+1}{k}\int_0^\infty (1-ks)_+^n ds = \sum_{k=1}^{n+1}(-1)^{k+1} \binom{n+1}{k}\int_0^{1/k}(1-ks)^n ds $$
$$=\frac{1}{n+1} \sum_{k=1}^{n+1}(-1)^{k+1} \frac{1}{k} \binom{n+1}{k}=\sum_{k=1}^{n+1}(-1)^{k+1} \frac{1}{k^2} \binom{n}{k-1}. $$
Here is $E_n$ answers for small $n$ (thank you MAPLE)
$$ E_1=\frac{3}{4},\;\;E_2=\frac{11}{18},\;\;E_3=\frac{25}{48},\;\;E_4=\frac{137}{300},\;\; E_5=\frac{49}{120}. $$
It turn out that $L_n$ is highly concentrated around its mean. In the work of P. Levy I mentioned earlier he showed that the random variables $nL_n-\log n$ converges in probability to a random variable $X_\infty$ with probability distribution $\mu$ given by
$$ \mu\bigl(\,(-\infty,x])= \exp\bigl(\,-e^{-x}\,\bigr),\;\;x\geq 0.$$
Moreover
$$\lim_{n\to \infty} \bE[\, nL_n-\log n\,]=\gamma=\bE[X_\infty],\;\;\lim_{n\to \infty}\mathrm{Var}[ nL_n\,]=\frac{\pi^2}{6}=\mathrm{Var}[X_\infty]. $$
$$\frac{n}{\log n} L_n \to 1\;\; \mbox{a.s.} $$
Note that this shows that
$$E_n\sim\frac{\log n}{n}\;\; \mbox{as $n\to \infty$}. $$
I'll stop here, but you can learn more from this paper of Luc Devroye and its copious list of references.
Denote by $A_n$ the smallest spacing
$$ A_n:=\min_{1\leq k\leq n+1} S_k. $$.
Note that
$$\bP[ A_n>a]=\bP[ S_1,S_2,\dotsc, S_{n+1}>a]=\big( 1-(n+1)a\big)^n_+. $$
Hence
$$ \bE[ A_n]=\int_0^\infty\bP[A_n>a] da= \int_0^\infty \big( 1-(n+1)a\big)^n_+ da=\int_0^{\frac{1}{n+1}} (1-(n+1)a)^n da$$
$$ = \frac{1}{n+1}\int_0^1 (1-t)^n dt= \frac{1}{(n+1)^2}. $$
Saturday, November 7, 2015
The Luzin affair
I was not aware that Luzin was persecuted by Stalin and some of his detractors were big names like Kolmogorov and Sobolev.
"Aleksandrov, Kolmogorov and some other students of Luzin accused him of plagiarism and various forms of misconduct. Sergei Sobolev and Otto Schmidt incriminated him with charges of disloyalty to Soviet power. "
Nikolai Luzin - Wikipedia, the free encyclopedia
"Aleksandrov, Kolmogorov and some other students of Luzin accused him of plagiarism and various forms of misconduct. Sergei Sobolev and Otto Schmidt incriminated him with charges of disloyalty to Soviet power. "
Nikolai Luzin - Wikipedia, the free encyclopedia
Subscribe to:
Posts (Atom)